Scale and Spatial Data Aggregation

-

 Scale and Spatial Data Aggregation

Levels of Detail

In spatial data analysis, scale and data aggregation are critical factors that influence the outcome of geographic studies and decision-making processes. Both play a vital role in determining how geographic phenomena are recorded, represented, and understood. 

Scale

Scale in the context of spatial data refers to spatial extent or the level of detail that geographic features are recorded and represented. Scale can be understood as the ratio of what is featured on the map and what occurs in the real world. It is impossible to record every microscopic detail of the land or every nuance of nominal study features. Spatial analysts must determine the level of data smoothing required for a project. 

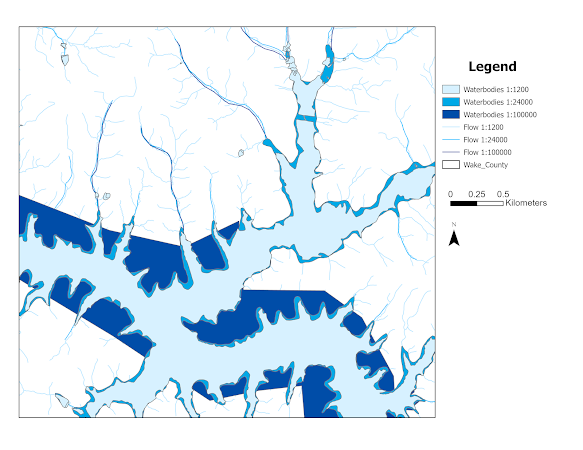
In geographic studies, as scale changes, so too do the features of the landscape. The simple map below records water features for the same study area and compares them at three levels of scale. As coarseness increases, smaller features are lost completely and boundaries are simplified. This results in shorter perimeters, simplified polygons, and larger surface areas. In DEMS we would see elevation smoothing and a decrease in average slope. 

Spatial Data Aggregation

Every spatial analysis requires some level of data aggregation, which combines and summarizes data to make it manageable. However, every choice of scale and unit boundaries (zoning) results in the Modifiable Areal Unit Problem (MAUP). Analysis outcomes are dependent on scale and data aggregation. Statistical bias occurs every time spatial data is aggregated.


The same variables but aggregated in different ways results in different slope, intercept, r-value.

Gerrymandering

How a district is created impacts election outcomes. Designers must contend with not just geography but the vast array of demographic variables. Ideally, the district boundary encircles a singular area of interest. A perfectly circular boundary is considered optimally compact. In reality, we frequently see strange shapes. These seemingly arbitrary boundaries are potentially gerrymandering, which takes advantage of voting aggregation to result in biased elections. Using scores such as the Polsby-Popper Ratio can help us mathematically define the compactness of a district. 

Though not circular, this district presents high compactness

A distinct with little compactness

Further Reading:


Comments

Post a Comment

Popular posts from this blog

Coastal Flooding & Storm Surge Analysis

-
Image
     As climate change continues to intensify storms and increase flooding, it is vital for communities and governments to prepare for inevitable storm damage. In this week's lab, we explored coastal flooding models and prepared our own storm surge analysis. Our study area was Mantoloking, New Jersey, a low-laying barrier island that suffered major damage from superstorm Sandy in 2012. More information about the storm can be found on New Jersey's Department of Environmental Protection . Superstorm Sandy     By comparing LiDAR data before and a few days after the storm, we can create a comparison analysis. The LiDAR data is converted into a DEM by first creating a TIN (triangulated irregulated network). As the TIN shows, the topography varies little with only very mild sloping.  LiDAR .las point cloud dataset is converted into a  TIN       By subtracting the two DEMS, we can see the changes in the environment. Further color manipulation makes it clear where land has eroded or be
Read more

Welcome to GIS 5007 Spring 2023

-
Image
My name is Kelsey Yoder-Ostroski and I am a new(er) student in the world of GIS. This is my third class in UWF's GIS Admin graduate program as a full-time student. At the moment I am a caregiver to our kids but I also do volunteer work with a nonprofit providing support to local moms. We are a military family; we have lived in the Navarre area for 3 years and are preparing to move to Germany this summer. I'm not ready for the cold! I am originally from Texas so I love the heat, but we can't wait to see everything Germany and its neighbors have to offer.  In my free time, I enjoy learning German, baking (mostly breads), or doing home improvement projects. I have a weakness for cookies and power tools.  I am pursuing a master's in GIS business administration because I love how applicable and versatile it is. It literally encompasses every topic on Earth from the land to its resources and to all of history. I'm not 100% sure what I will do after graduating but I am int
Read more

Introduction to Python

-
Image
As an introduction to Python, which is a computing language that is embedded in ArcGIS Pro, we were tasked with creating a flow chart and pseudocode for converting radians into degrees. Flowcharts are a visual method of planning, which is an especially important process to complete before delving into complicated code. Flowchart created in iodraw.com The aim of this exercise was to introduce us to calling up IDLE and ArcGIS Notebooks. IDLE looks like the stereotypical coding interface with its intimating emptiness and blocky text; whereas Notebooks is nearly the opposite with its bright, white interface, menu options, and bubbly outlining. Both programs act as language interpreters for the Python coding language, converting user commands into binary which is then read and executed by the computer processing system. 
Read more